return to main 1401 Restoration Page
Comments on "CT 1401 runs FORTRAN compiler!"
Comments about
The IBM 1401 compiles and runs FORTRAN II video by CuriousMarc - posted Feb 2, 2018
The heroes
- Mike Albaugh -Docent in movie (and a major factor in this local effort )
- CuriousMarc (Marc Verdiell) - Narrator (& script, photographer, editor, ...)
- Van Snyder, and Paul Pierce - (Remote, Hidden way behind the scenes) -
The presentation is in two parts - each about 12 minutes
a) the first FORTRAN compile and run
b) some "behind the scenes" activities "for hard core fans"
Table of Contents
- Compiler Overlays
- Parameter Card
- Example Code
- Steps in the demo video - part 1
- Compile & Go
- A Collection of Comments
- A Tale about Hilbert Matrix
Compiler Overlays
As noted in several places on this web site, the FORTRAN compiler tape
uses 63 overlays, which should be visible as pauses in reading the compiler from tape.
The 63 overlays to allow compilation in a small (8,000 character) 1401 memory.
from
1401-IBM-Systems-Journal-FORTRAN.html
|
The 1401 FORTRAN compiler was designed for a minimum of 8000 positions of core, with tape usage being optional. The fundamental design problem stems from the core storage limitation. Because the average number of instructions per phase and the number of phases selected are inversely related (at least to a significant degree), the phase organization was employed to circumvent the core limitation. The 1401 FORTRAN compiler has 63 phases, an average of 150 instructions per phase, and a maximum of 300 instructions in any phase.
|
Overlays are not used much anymore because even Windows fits into the usual 4 gigabyte memories
available for about $40 in 2018.
(Mike Albaugh points out that modern computers also have an MMU
-Memory Management Unit- available to help handle these enormous memories)
More details about the overlays are available in
-
Fortran-v3m0-listing/Fortran-v3m0-listing.html
- 1401-FORTRAN-Illustrated.html
|
Parameter Card
Mike e-mailed ---- About the PARAM card ----
Note that the first and third characters of the options
are zoned, as I9Z .
According to C24-1455-2 (1401 Fortran spec) the PARAM
card (actually called the control card, see Pg 26).
is as follows:
COLS value meaning
1-5 PARAM identifies card
6-8 maxadr 1401-style address of top of memory
must be <= size of memory of build/run machine
9-10 K 1-20, number of digits in integer (default 5)
11-12 F 1-20, digits in mantissa of float (default 8)
13 P to punch out a condensed object deck
14 S if storage snapshot desired
15 T if compiling on 1410 in 1401 compat mode
16 FMT various options for FORMAT routine:
X None
L Limitted (tape read/write only)
blank if normal.
A include A conversions

| |
Example Code
FORTRAN code "first example in the manual" - page 44
C24-1455-2_Fortran_Specifications_and_Operating_Procedures_Apr65.pdf
in BitSavers.org
Sequence Card
# Columns
0000000001111111111222222222233333333334444444444
1234567890123456789012345678901234567890123456789
01 PARAMI9Z0515
02 C MATRIX ARITHMETIC
03 DIMENSION A(7,7), VECTOR(7), b(7,7)
...
N END
N+1 - blank card for card reader -
This is the complete source code used by Mike Albaugh
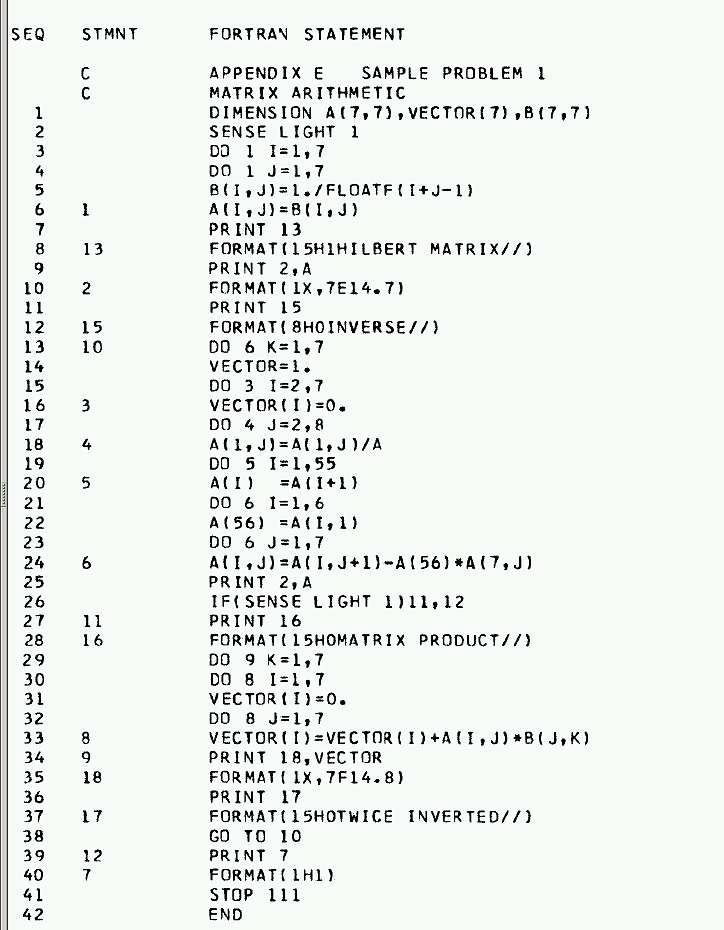
|
Steps in the demo video - part 1
- Tape 1 - "freshly made" Compiler
- Compiled card source code in 1402
- Ran the FORTRAN compiled code which was left in memory (a compile option)
-
Output to 1403 Printer
|

|
Compile & Go
Mike Albaugh e-mailed
"1401 FORTRAN allowed "compile and go", where
the compiled code (still in core from the compilation step)
could be immediately run without punching an object deck.
A valuable feature for student (and old guys who have forgotten
quite a bit) programs. "Save a tree. Punch out only code that
will actually run."
We did that. If the PARAM line had included a 'P' after the
0515 (5-digit integers, 15-digit mantissas for floats), the
compiler would have punched an object deck.
|
A Collection of Comments
from Van Snyder
|
> FORTRAN may have even broader appeal than the IBM 1401.
One of the nice features of 1401 Fortran is that you can choose up to
twenty digits for the mantissa, and the floating-point implementation
automagically carries two more guard digits. It doesn't do symmetric
rounding, but it is actually much better arithmetic than anything that
appeared before IEEE.
Thanks, Gary Mokotoff!
It uses the printer area for the accumulator, so there's room for a
longer mantissa.
|
Mike Albaugh replying to Ron Mak
|
> And what an amazing coincidence: I’ve attached this week’s programming assignment for my C++ class. Does the FORTRAN output match the C++ output?
Unlikely, since the Fortran example uses a 7x7 Hilbert matrix.
Also, as Van has pointed out, it use a 15-digit mantissa (about
50 bits), so IEEE single floats are unlikely to "match". As are
IEEE Doubles, as anyone who has read
"What Every Computer Scientist Should Know About Floating Point"
(widely available, including at
http://www.lsi.upc.edu/~robert/teaching/master/material/p5-goldberg.pdf )
Should know. :-)
I'll leave it to others to find and reference Von Neumann's comments
on FP. And Seymour Cray's, for that matter.
-Mike
Ron Mak replied
|
Mike Albaugh replying to Ed Thelen
> FORTRAN may have even broader appeal than the IBM 1401.
>
> Process control people really liked FORTRAN because
> it was hard to get yourself into trouble.
You may not have been trying hard enough.
Just as a Real Programmer (tm) can write Fortran in any language,
so can one write Intercal (or TECO) in any language.
> No forgetting to return memory from malloc(),
> - no forgetting to initialize pointers,
> - no messing up inheritance,
> - no easy way to shoot your foot off, even if you wanted to.
You have not kept up with Modern Fortran.
> Maybe not as safe as ADA,
> but certainly lacking the potential traps & pit-falls of say C++
>
> I better not say more,
> not wishing to start a major flame war -
I'll bite. Now, should my battle Cry be "Laugh while you can, Monkey Boy"
or "Don't get cocky, kid"? (I keep messing up my cult movie references).
Anyway, the particular Example Program used in the video is in fact
an _example_ of how _not_ to write reliable code in Fortran. In several
places it blithely refers to a 2D array with only one subscript, that
varies over more than the product of the dimensions of the array, thus
assuming that the "adjacent in the source code" 1D array is "adjacent
in memory" (and at the expected "end" of the merged array".
As Ken Thompson would say "Unwarranted chumminess with the compiler"
I am in the process of modifying the code to be less terrifying and
still capable of being compiled and run. One discovery gives me a clue
about why it was coded this way: If I fix even some of the most egregious
hacks, it will not compile/run on an 8K 1401. I had to bump the PARAM
card to I9Z (12K) to do it. So, I _suspect_ that someone copied an
example out of a textbook, but was ordered to "make it fit in 8K",
and, well, we've all been there, right? Please tell me I am not
the only one ever ordered to "cut corners". Also, please tell me I
am not the only one to threaten to quit in those circumstances.
-Mike
|
Mike Albaugh replying to Van Snyder
> One of the nice features of 1401 Fortran is that you can choose up to
> twenty digits for the mantissa, and the floating-point implementation
> automagically carries two more guard digits.
IIRC, 1620 Fortran allowed up to 28 mantissa digits (I recall the
control card being FANDK, where FANDK2802 was not uncommon). It also
allowed specification of the "noise" digit to be used during normalization.
Run once with a 0 and once with a 9, it provided a sort of
"Poor Man's Interval Arithmetic". Not that a poor person could
afford a 1620, or a 1401, but students are often awake at hours
when computers are lightly used.
-Mike
|
from Ron Mak to Michael Albaugh
It may be interesting to compare, anyway. Yes, I used doubles in my calculations. I used scaling and partial pivoting in the LU decomposition to minimize round-off errors.
The round-off errors are most visible in the inverse. All the elements of a Hilbert inverse should be whole numbers.
– Ron
P.S. My assignment is for a class of 80 graduate computer engineering students. None of them had heard of Hilbert matrices and only one knew about LU decomposition.Do undergrads still take linear algebra and numerical methods? Kids nowadays ...
Hilbert7fixed.txt
Hilbert matrix of size 7:
1.000000 0.500000 0.333333 0.250000 0.200000 0.166667 0.142857
0.500000 0.333333 0.250000 0.200000 0.166667 0.142857 0.125000
0.333333 0.250000 0.200000 0.166667 0.142857 0.125000 0.111111
0.250000 0.200000 0.166667 0.142857 0.125000 0.111111 0.100000
0.200000 0.166667 0.142857 0.125000 0.111111 0.100000 0.090909
0.166667 0.142857 0.125000 0.111111 0.100000 0.090909 0.083333
0.142857 0.125000 0.111111 0.100000 0.090909 0.083333 0.076923
Hilbert matrix inverted:
49.000000 -1176.000003 8820.000026 -29400.000100
48510.000185 -38808.000160 12012.000053
-1176.000003 37632.000106 -317520.001023 1128960.003993
-1940400.007343 1596672.006359 -504504.002092
8820.000025 -317520.001014 2857680.009822 -10584000.038333
18711000.070474 -15717240.061028 5045040.020072
-29400.000098 1128960.003931 -10584000.038073 40320000.148565
-72765000.273099 62092800.236470 -20180160.077768
48510.000179 -1940400.007189 18711000.069623 -72765000.271644
133402500.499301 -115259760.432298 37837800.142161
-38808.000154 1596672.006200 -15717240.060032 62092800.234198
-115259760.430439 100590336.372654 -33297264.122541
12012.000051 -504504.002032 5045040.019674 -20180160.076748
37837800.141048 -33297264.122107 11099088.040151
Hilbert matrix multiplied by its inverse:
1.000000 -0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
0.000000 1.000000 0.000000 0.000000 0.000000 0.000000 -0.000000
-0.000000 -0.000000 1.000000 0.000000 -0.000000 -0.000000 -0.000000
0.000000 0.000000 -0.000000 1.000000 -0.000000 -0.000000 -0.000000
0.000000 -0.000000 0.000000 0.000000 1.000000 -0.000000 0.000000
0.000000 -0.000000 -0.000000 0.000000 -0.000000 1.000000 -0.000000
-0.000000 0.000000 -0.000000 0.000000 -0.000000 0.000000 1.000000
Inverse Hilbert matrix inverted:
1.000000 0.500000 0.333333 0.250000 0.200000 0.166667 0.142857
0.500000 0.333333 0.250000 0.200000 0.166667 0.142857 0.125000
0.333333 0.250000 0.200000 0.166667 0.142857 0.125000 0.111111
0.250000 0.200000 0.166667 0.142857 0.125000 0.111111 0.100000
0.200000 0.166667 0.142857 0.125000 0.111111 0.100000 0.090909
0.166667 0.142857 0.125000 0.111111 0.100000 0.090909 0.083333
0.142857 0.125000 0.111111 0.100000 0.090909 0.083333 0.076923
|
|
A tale about the "Hilbert Matrix" used as a test problem above.
(Shown on the 1403 printer, above)
| Long ago (1967) and far away (Minnesota) there was a then famous computer company called
Control Data Corporation (CDC).
I (Ed Thelen) was a new employee in its Special Systems Division - and witnessed the following:
Our group was competing for business from the Naval Research Lab. Part of the proposal
was to time and otherwise verify that "we" could do the usual transformations on
a "Hilbert Matrix" supplied as a FORTRAN deck by the Navy. But we were getting somewhat different answers
than those supplied by the Navy.
Fortunately for me (I've had much luck :-) the challenge was given to another person.
After week or two struggle, that other person determined that:
- The answers we had been given were "wrong". The matrix operations had been computed in
IBM 360 single precision floating point (32 bits including fraction and exponent)
(the unsigned 24 bit fraction is accurate to about 7 decimal places)
- "Our" answers were much better, having been computed using the
standard CDC 6600 floating point -
(60 bits including coefficient and exponent) (the unsigned 48 bit coefficient being accurate to
about 15 decimal places)
- A comment from Wikipedia
"The Hilbert matrices are canonical examples of ill-conditioned matrices,
making them notoriously difficult to use in numerical computation.
For example, the 2-norm condition number of the matrix above is about 4.8*105."
Due to this, plus the fact that we were very good at linking to the analog world to do the digital part of
"hybrid" computing,
helped give us the contract :-))
I wonder if the 1401 test problem was similar to that provided by the Navy to CDC so many years ago.
Note that the 1401 floating point used the default 8 decimal digit mantissa (precision)
|


